그래프를 저장하는 방법
그래프는 우리 생활에서 자주 사용하는 개념은 아니지만, 컴퓨터 관련 공부를 하게 된다면 적어도 한번은 다루는 중요한 개념 중 하나이다.
이 그래프를 c언어, c++ 등의 컴퓨터 언어로 나타내는 방법은 어떤 방법이 있을까?
1 그래프의 구성 및 종류
그래프를 구성하는 요소들은 다음과 같다
-정점(vertex / node) : 정점은 그래프의 구성요소 중 하나로 어떤 위치라는 개념을 뜻한다.
-간선(edge / link) : 간선은 정점과 정점을 잇는 역할을 하며 방향성의 유무에 따라 표기법이 다르다.
-가중치(weight) : 간선이 가진 가치, 혹은 cost를 나타내는 개념이며 그래프에서는 간선 위 숫자가 가중치를 뜻한다.
그래프를 간단하게 나눈다면 총 2가지 종류의 그래프로 나눌 수 있다.
-Directed Graph(단방향 그래프) : 방향성이 존재하는 그래프를 의미하며, 간선에 방향성이 존재하는 그래프를 뜻한다. 따라서 그래프를 그릴 때 화살표 표시를 이용하여 그래프의 방향성을 나타내 주어야 한다.
-Undirected Graph(양방향 그래프) : 방향성이 존재하지 않는 그래프를 의미하며, 간선에 방향성이 없는 그래프를 뜻한다. 그래프를 그릴 때에는 단순하게 정점과 정점을 이어주는 선으로 나타낸다.
출처: https://www.leafcats.com/77
2 그래프의 저장(2차원 배열)
본격적으로 그래프를 저장하는 방법을 설명하도록 하겠다.
우선 그래프를 저장하는 중에서도 가장 간단한 방법인 2차원 배열을 이용하여 그래프를 저장하는 방법이다.
각 정점(node)들에 번호를 부여한 후 해당 정점들 사이에 간선이 존재하면 1을 표시하며 간선이 존재하지 않을 경우 0으로 표시한다.
단, 가중치가 존재할 경우에는 1대신 가중치를 넣어주면 된다.
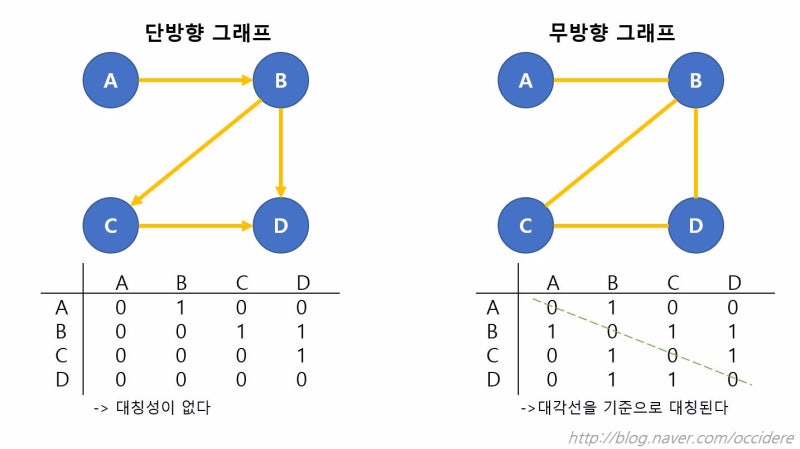
출처: https://m.blog.naver.com/occidere/220923695595
장점 : 직관적이며 구현이 어렵지 않다.
단점 : 불필요한 정보 및 공간이 많이 든다.(0으로 된 부분들이 전부 필요없는 부분)
3 벡터를 이용한 그래프 저장(가중치 X)
벡터는 배열과 다르게 자료를 넣을 떄 마다 공간이 늘어나기 때문에 필요한 정보만을 저장할 수 있다.
이 때는 2차원배열처럼 두 node에 해당하는 칸에 간선의 정보를 넣는 것이 아닌, 간선이 시작하는 node에 간선의 정보를 저장한다.

출처: https://m.blog.naver.com/occidere/220923695595
위 그래프의 경우, 알파벳으로 쓰여있는 정점은 저장하기 어렵기 때문에 숫자로 나타내었다고 가정하면 A번 정점은 1번정점, B번은 2번정점, … 이런식으로 배열에 저장될 것이다.
이 때 2차원 배열에서 저장할 때는 arr[1][2] = 1; 이런식으로 저장했지만
vector를 사용할 경우에는 v[1].push_back(2) 이런식으로 출발하는 node에 도착지의 정보를 저장한다.
이렇게 사용했을때 1번 정점과 간선이 연결이 되어있지 않은 3번 정점의 경우에는 vector에 저장되지 않는 것을 알 수 있다.
즉, 불필요한 정보를 저장하지 않기 때문에 2차원 배열보다 더 적은 공간을 사용하므로 보다 효율적인 방법인 것이다.
아래 코드는 가중치가 없을 때 vector를 이용하여 그래프를 저장할 수 있는 코드이다.
#include <stdio.h>
#include <vector>
using namespace std;
/*-----------------------------------------------------------------------------------
vector를 선언할 때 2차원배열과 비슷한 방식으로 저장하기 때문에 2차원 vector를 이용한다.
이 때 vector배열의 최대 크기는 node개수이며 vector의 자료형은 도착정점의 정보만 필요하므로 int형이다.
------------------------------------------------------------------------------------*/
vector<int> v[505];
int main() {
//이때 n은 node의 개수, m은 edge개수를 의미한다.
int n, m;
//edge개수만큼 입력을 받는다.
for(int i = 0; i < m; i++){
// a는 from(출발지), b는 to(도착지)를 의미한다.
int a, b;
scanf("%d %d", &a, &b);
v[a].push_back(b); //단방향일때 이 부분만 사용
v[b].push_back(a); //양방향일때 이 부분까지 사용해야함
}
//그래프를 탐색하거나 이용할 때 주로 사용하는 코드
//1번 node부터 n번 node까지 전부 탐색한다
for(int i = 1; i <= n; i++){
//해당 node에서 갈 수 있는 모든 간선의 정보가 저장되어있다.
for(int j = 0; j < v[i].size(); j++){
//next는 i번 node와 연결되어있는 node의 정보를 하나씩 저장한다.
//이 때 next의 자료형은 vector의 자료형과 같아야한다.
int next = v[i][j];
//이후 사용할 내용
}
}
return 0;
}
4 벡터를 이용한 그래프 저장(가중치 O)
가중치가 존재할 경우에는 vector에 한가지 정보가 아닌 가중치를 포함하여 2가지 정보를 저장해야한다.
따라서 기존의 int형 vector로는 저장할 수 없다.
이 때 사용할 수 있는 것이 구조체와 pair 개념이다.
pair를 간단하게 설명하자면 하나의 지료형에 2개의 자료형을 넣은 형태인데 이는 나중에 다루도록 하겠다.
구조체도 pair와 마찬가지로 여러 변수와 함수를 저장할 수 있는 일종의 컨테이너와 같은 역할을 하는데 구조체 또한 지난학기 스터디에 다루었기 때문에 아래 코드에서만 간단하게 설명만 하고 넘어가도록 하겠다.
구조체가 아직 이해가 안될 경우를 위해 지난학기에 유튜브에 올렸던 강의링크를 올리도록 하겠다.
(그래도 혹시 이해가 안된다면 카카오톡으로 질문해주세요 ^_^ 유튜브링크)
이제 구조체를 이해했다고 가정하고 가중치를 포함한 그래프를 저장하는 방법을 설명하도록 하겠다.
출처: https://www.leafcats.com/77
앞에서도 말했듯이 위 사진과 같이 가중치가 있는 그래프를 저장할 경우에는 vector에 2가지 이상의 정보를 저장해야한다.
예를들어 위 그래프의 경우, 2차원 배열에서 저장할 때는 arr[1][4] = 8; 이런식으로 저장했지만
vector를 사용할 경우에는 v[1].push_back({4, 8}); 이런식으로 출발하는 node에 도착지의 정보와 가중치를 함께 저장한다.
위와 같이 중괄호를 이용하여 구조체를 한꺼번에 저장할 수 있다.
아래 코드는 가중치를 포함한 그래프를 저장하고 사용할 수 있는 코드이다.
#include <stdio.h>
#include <vector>
using namespace std;
typedef struct Node{
int to, cost;
};
/*-----------------------------------------------------------------------------------
vector를 선언할 때 2차원배열과 비슷한 방식으로 저장하기 때문에 2차원 vector를 이용한다.
만약 간선에 가중치가 있을 경우 구조체를 이용하거나 pair<>를 이용하여 저장할 수 있다.
이 때 vector배열의 최대 크기는 node개수이다.
------------------------------------------------------------------------------------*/
vector<Node> v[505];
int main() {
//이때 n은 node의 개수, m은 edge개수를 의미한다.
int n, m;
//edge개수만큼 입력을 받는다.
for(int i = 0; i < m; i++){
// a는 from(출발지), b는 to(도착지), c는 cost(가중치)를 의미한다.
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
v[a].push_back({b, c}); //단방향일때 이 부분만 사용
v[b].push_back({a, c}); //양방향일때 이 부분까지 사용해야함
}
//그래프를 탐색하거나 이용할 때 주로 사용하는 코드
//1번 node부터 n번 node까지 전부 탐색한다
for(int i = 1; i <= n; i++){
//해당 node에서 갈 수 있는 모든 간선의 정보가 저장되어있다.
for(int j = 0; j < v[i].size(); j++){
//next는 i번 node와 연결되어있는 간선의 정보를 하나씩 저장한다.
//이 때 next의 자료형은 vector의 자료형과 같아야한다.
Node next = v[i][j];
//이후 사용할 내용
}
}
return 0;
}

